Advanced Mechanics Of Materials And Applied Elasticity

Foreword

This text is an outgrowth of the material used by the author for several decades in senior and graduate courses for students of mechanical, aerospace and civil engineering. It deals with the problem of computing the stress and displacement fields in solid bodies at two levels of approximation: the level of the linear theory of elasticity and the level of the theories of mechanics of materials. The linear theory of elasticity is based on very few assumptions and can be applied to bodies of any geometry. The theories of mechanics of materials are based on many assumptions in addition to those of the theory of elasticity and they can be applied only to bodies of certain geometries (beams, bars, shafts, frames, plates shells and thin-walled, tubular members). In this text the formulas of the theories of mechanics of materials are derived in a way that the assumptions on which they are based can be clearly understood. Moreover, wherever possible the results obtained on the basis of the theories of mechanics of materials are compared with those obtained on the basis of the
theory of elasticity.

In the past, the use of the linear theory of elasticity was limited by the fact that only a few problems could be solved using the available classical methods. Thus, approximate theories like the theories of mechanics of materials were formulated for which exact solutions could be found. With the advent of the electronic computer, many problems involving bodies whose geometry does not justify the use of the theories of mechanics of materials, are formulated on the basis of the linear theory of elasticity and solved approximately with the aid of a computer. Thus, a mechanical, civil or aerospace engineer who works in the area of stress analysis and design often uses software based on the linear theory of elasticity. It is important therefore that master’s level students of mechanical, aerospace and civil engineering who specialize in the area of stress analysis and design, should acquire some knowledge of applied elasticity. The book includes 18 chapters and 7 appendices. In the first chapter a brief review of vector analysis is presented followed by a very elementary, but concise introduction to the algebra of symmetric tensors of the second rank. In the theories of mechanics of materials and elasticity one deals with quantities such as stress, strain and moments and product of inertia which are symmetric tensors of the second rank. It is desirable therefore that the student learns at the very beginning the transformation properties of such quantities as well as how to determine their stationary values.

The boundary value problems for computing the displacement and stress fields in solid bodies on the basis of the linear theory of elasticity, are formulated in Chapter 5 and applied to simple examples in Chapters 5, 6 (torsion problem) and 7 (plain stress and plain strain problems). The boundary value problems for computing the displacement and stress fields in the basis of the theory of mechanics of materials are presented in Chapters 8 and 9 for bodies made of prismatic line members, in Chapter 10 for nonprismatic line members, in Chapter 11 for curved line members, in Chapter 12 for tubular members and in Chapters 17 for plates. Part of the material presented in Chapters 8 and 9 is available in elementary texts of strength of materials. It is included in this text for completeness of our presentation and for those who need a review of this material at a slightly more advanced level than that of the elementary texts. In this text, the boundary value problems for computing the displacement and stress fields in solid bodies are formulated using both their differential and integral forms (see Chapters 13 and 14). The latter include the principle of virtual work, Castigliano’s second theorem, the theorem of minimum total potential energy, the weighted residual equation and the modified weighted residual equation. The last three are suitable for obtaining numerical solutions of boundary value problems with the aid of a computer, using the finite element method presented in Chapter 15. With the exception of Chapter 16, where an introduction to plastic analysis of structures is presented, throughout this text, we limit our attention to bodies made from isotropic linearly elastic materials. Moreover, with the exception of Chapter 18, where an introduction to elastic instability of structures is presented, we assume that the magnitude of the deformation of each material particle of the bodies, which we are considering, is such that the change of its geometry can be approximated by its components of the strain tensor which are related to its components of displacement by linear relations. This assumption linearizes the boundary value problems involving bodies made from linearly elastic materials, that is, renders the effect linearly related to the cause and permits superposition of the results.

The author wishes to thank Dr. Nikitas Skliros for typing and laying out the final version of the manuscript and Mr. Nassos Papoutsis for drawing and labeling the figures. Moreover, the author wishes to thank Ms. Cleo Avrithy for checking the solution presented in the solution manual of the problems included at the ends of Chapters 1 to 10 and Ms. Isabella Vassilopoulou for checking the solution presented in the solution manual of the problems included at the ends of Chapters 11 and 13 to 17.

Chapter 1 Cartesian Tensors

1.1 Vectors

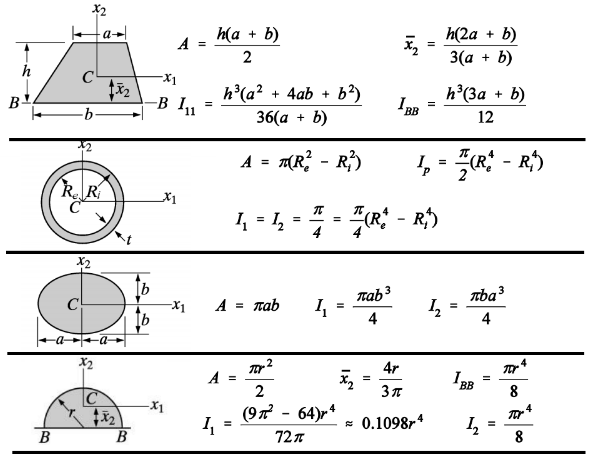
In order to specify completely certain physical quantities, such as temperature, energy and mass, it is necessary to give only a real number. These quantities are referred to as scalars. In order to specify completely certain other physical quantities, such as force, moment, velocity and acceleration, it is necessary to give both their magnitude (a nonnegative number), their direction and their sense. These quantities are referred to as vectors. They may be represented in a three-dimensional, Euclidian space by directed line segments (arrows) whose length is proportional to the magnitude of the vectors and whose direction and sense are those of the vectors. Two vectors are equal if they have the same magnitude, direction and sense. One way of denoting vector quantities is by boldface Latin letters, i.e., a, b, c, whereas their magnitude is represented as a,b and c, respectively.

The sum of two vectors a and b, as, for example, of two forces or of two velocities, is a vector c, which is specified (as shown in Fig. 1.1) by the diagonal of the parallelogram having as adjacent sides the vectors a and b. This rule of addition of two vectors is referred to as the parallelogram rule. The negative of a vector a is a vector !a having the magnitude and direction of a and reverse sense. Any vector whose magnitude is equal to unity is referred to as a unit vector. Every vector a n may be expressed as the product of its magnitude and the unit vector i having the same direction and sense as the vector a.

Table of Contents

Chapter 1 Cartesian Tensors

• 1.1 Vectors
• 1.2 Dyads
• 1.3 Definition and Rules of Operation of Tensors of the Second Rank
• 1.4 Transformation of the Cartesian Components of a Tensor of the Second Rank upon Rotation of the System of Axes to Which They Are Referred
• 1.5 Definition of a Tensor of the Second Rank on the Basis of the Law of Transformation of Its Components
• 1.6 Symmetric Tensors of the Second Rank
• 1.7 Invariants of the Cartesian Components of a Symmetric Tensor of the Second Rank
• 1.8 Stationary Values of a Function Subject to a Constraining Relation
• 1.9 Stationary Values of the Diagonal Components of a Symmetric Tensor of the Second Rank
• 1.10 Quasi Plane Form of Symmetric Tensors of the Second Rank
• 1.11 Stationary Values of the Diagonal and the Non-Diagonal Components of the Quasi Plane, Symmetric Tensors of the Second Rank
• 1.12 Mohr’s Circle for Quasi Plane, Symmetric Tensors of the Second Rank
• 1.13 Maximum Values of the Non-Diagonal Components of a Symmetric Tensor of the Second Rank
• 1.14 Problems

Chapter 2 Strain and Stress Tensors

• 2.1 The Continuum Model
• 2.2 External Loads
• 2.3 The Displacement Vector of a Particle of a Body
• 2.4 Components of Strain of a Particle of a Body
• 2.5 Implications of the Assumption of Small Deformation
• 2.6 Proof of the Tensorial Property of the Components of Strain
• 2.7 Traction and Components of Stress Acting on a Plane of a Particle of a Body
• 2.8 Proof of the Tensorial Property of the Components of Stress
• 2.9 Properties of the Strain and Stress Tensors
• 2.10 Components of Displacement for a General Rigid Body Motion of a Particle
• 2.11 The Compatibility Equations
• 2.12 Measurement of Strain
• 2.13 The Requirements for Equilibrium of the Particles of a Body
• 2.14 Cylindrical Coordinates
• 2.15 Strain–Displacement Relations in Cylindrical Coordinates
• 2.16 The Equations of Compatibility in Cylindrical Coordinates
• 2.17 The Equations of Equilibrium in Cylindrical Coordinates
• 2.18 Problems

Chapter 3 Stress–Strain Relations

• 3.1 Introduction
• 3.2 The Uniaxial Tension or Compression Test Performed in an Environment of Constant Temperature
• 3.3 Strain Energy Density and Complementary Energy Density for Elastic Materials Subjected to Uniaxial Tension or Compression in an Environment of Constant Temperature
• 3.4 The Torsion Test
• 3.5 Effect of Pressure, Rate of Loading and Temperature on the Response of Materials Subjected to Uniaxial States of Stress
• 3.6 Models of Idealized Time-Independent Stress–Strain Relations for Uniaxial States of Stress
• 3.7 Stress–Strain Relations for Elastic Materials Subjected to Three-Dimensional States of Stress
• 3.8 Stress–Strain Relations of Linearly Elastic Materials Subjected to Three-Dimensional States of Stress
• 3.9 Stress–Strain Relations for Orthotropic, Linearly Elastic Materials
• 3.10 Stress–Strain Relations for Isotropic, Linearly Elastic Materials Subjected to Three-Dimensional States of Stress
• 3.11 Strain Energy Density and Complementary Energy Density of a Particle of a Body Subjected to External Forces in an Environment of Constant Temperature
• 3.12 Thermodynamic Considerations of Deformation Processes Involving Bodies Made from Elastic Materials
• 3.13 Linear Response of Bodies Made from Linearly Elastic Materials
• 3.14 Time–Dependent Stress-Strain Relations
• 3.15 The Creep and the Relaxation Tests
• 3.16 Problems

Chapter 4 Yield and Failure Criteria

• 4.1 Yield Criteria for Materials Subjected to Triaxial States of Stress in an Environment of Constant Temperature
• 4.2 The Von Mises Yield Criterion
• 4.3 The Tresca Yield Criterion
• 4.4 Comparison of the Von Mises and the Tresca Yield Criteria
• 4.5 Failure of Structures — Factor of Safety for Design
• 4.6 The Maximum Normal Component of Stress Criterion for Fracture of Bodies Made from a Brittle, Isotropic, Linearly Elastic Material
• 4.7 The Mohr’s Fracture Criterion for Brittle Materials Subjected to States of Plane Stress
• 4.8 Problems

Chapter 5 Formulation and Solution of Boundary Value Problems Using the Linear Theory of Elasticity

• 5.1 Introduction
• 5.2 Boundary Value Problems for Computing the Displacement and Stress Fields of Solid Bodies on the Basis of the Assumption of Small Deformation
• 5.3 The Principle of Saint Venant
• 5.4 Methods for Finding Exact Solutions for Boundary Value Problems in the Linear Theory of Elasticity
• 5.5 Solution of Boundary Value Problems for Computing the Displacement and Stress Fields of Prismatic Bodies Made from Homogeneous, Isotropic, Linearly Elastic Materials
• 5.6 Problems

Chapter 6 Prismatic Bodies Subjected to Torsional Moments at Their Ends

• 6.1 Description of the Boundary Value Problem for Computing the Displacement and Stress Fields in Prismatic Bodies Subjected to Torsional Moments at Their Ends
• 6.2 Relations among the Coordinates of a Point Located on a Curved Boundary of a Plane Surface
• 6.3 Formulation of the Torsion Problem for Prismatic of Arbitary Cross Section on the Basis of the Linear Theory of Elasticity
• 6.4 Interpretation of the Results of the Torsion Problem
• 6.5 Computation of the Stress and Displacement Fields of Bodies of Solid Elliptical and Circular Cross Section Subjected to Equal and Opposite Torsional Moments at Their Ends
• 6.6 Multiply Connected Prismatic Bodies Subjected to Equal and Opposite Torsional Moments at Their Ends
• 6.7 Available Results
• 6.8 Direction and Magnitude of the Shearing Stress Acting on the Cross Sections of a Prismatic Body of Arbitrary Cross Section Subjected to Torsional Moments at Its Ends
• 6.9 The Membrane Analogy to the Torsion Problem
• 6.10 Stress Distribution in Prismatic Bodies of Thin Rectangular Cross Section Subjected to Equal and Opposite Torsional Moments at Their Ends
• 6.11 Torsion of Prismatic Bodies of Composite Simply Connected Cross Sections
• 6.12 Numerical Solutions of Torsion Problems Using Finite Differences
• 6.13 Problems

Chapter 7 Plane Strain and Plane Stress Problems in Elasticity

• 7.1 Plane Strain
• 7.2 Formulation of the Boundary Value Problem for Computing the Stress and the Displacement Fields in a Prismatic Body in a State of Plane Strain Using the Airy Stress Function
• 7.3 Prismatic Bodies of Multiply Connected Cross Sections in a State of Plane Strain
• 7.4 The Plane Strain Equations in Cylindrical Coordinates
• 7.5 Plane Stress
• 7.6 Simply Connected Thin Prismatic Bodies (Plates) in a State of Plane Stress Subjected on Their Lateral Surface to Symmetric 1 2 3 in x Components of Traction T and T 290 n n
• 7.7 Two-Dimensional or Generalized Plane Stress
• 7.8 Prismatic Members in a State of Axisymmetric Plane Strain or Plane Stress
• 7.9 Problems

Chapter 8 Theories of Mechanics of Materials

• 8.1 Introduction
• 8.2 Fundamental Assumptions of the Theories of Mechanics of Materials for Line Members
• 8.3 Internal Actions Acting on a Cross Section of Line Members
• 8.4 Framed Structures
• 8.5 Types of Framed Structures
• 8.6 Internal Action Release Mechanisms
• 8.7 Statically Determinate and Indeterminate Framed Structures
• 8.8 Computation of the Internal Actions of the Members of Statically Determinate Framed Structures
• 8.9 Action Equations of Equilibrium for Line Members
• 8.10 Shear and Moment Diagrams for Beams by the Summation Method
• 8.11 Stress–Strain Relations for a Particle of a Line Member Made from an Isotropic Linearly Elastic Material
• 8.12 The Boundary Value Problems in the Theories of Mechanics of Materials for Line Members
• 8.13 The Boundary Value Problem for Computing the Axial Component of Translation and the Internal Force in a Member Made from an Isotropic, Linearly Elastic Material Subjected to Axial Centroidal Forces and to a Uniform Change in Temperature
• 8.14 The Boundary Value Problem for Computing the Angle of Twist and the Internal Torsional Moment in Members of Circular Cross Section Made from an Isotropic, Linearly Elastic Material Subjected to Torsional Moments
• 8.15 Problems

Chapter 9 Theories of Mechanics of Materials for Straight Beams Made from Isotropic, Linearly Elastic Materials

• 9.1 Formulation of the Boundary Value Problems for Computing the Components of Displacement and the Internal Actions in Prismatic Straight Beams Made from Isotropic, Linearly
• Elastic Materials
• 9.2 The Classical Theory of Beams
• 9.3 Solution of the Boundary Value Problem for Computing the Transverse Components of Translation and the Internal Actions in Prismatic Beams Made from Isotropic, Linearly Elastic Materials Using Functions of Discontinuity
• 9.4 The Timoshenko Theory of Beams
• 9.5 Computation of the Shearing Components of Stress in Prismatic Beams Subjected to Bending without Twisting
• 9.6 Build-Up Beams
• 9.7 Location of the Shear Center of Thin-Walled Open Sections
• 9.8 Members Whose Cross Sections Are Subjected to a Combination of Internal Actions
• 9.9 Composite Beams
• 9.10 Prismatic Beams on Elastic Foundation
• 9.11 Effect of Restraining the Warping of One Cross Section of a Prismatic Member Subjected to Torsional Moments at Its Ends
• 9.12 Problems

Chapter 10 Non-Prismatic Members — Stress Concentrations

• 10.1 Computation of the Components of Displacement and Stress of Non-Prismatic Members
• 10.2 Stresses in Symmetrically Tapered Beams
• 10.3 Stress Concentrations
• 10.4 Problems

Chapter 11 Planar Curved Beams

• 11.1 Introduction
• 11.2 Derivation of the Equations of Equilibrium for a Segment of Infinitesimal Length of a Planar Curved Beam
• 11.3 Computation of the Circumferential Component of Stress Acting on the Cross Sections of Planar Curved Beams Subjected to Bending without Twisting
• 11.4 Computation of the Radial and Shearing Components of Stress in Curved Beams
• 11.5 Problems